회귀 모델 성능 평가
from sklearn.model_selection import cross_val_predict
y_valid_pred = cross_val_predict(model, X_train, y_train, cv=5, n_jobs=-1, verbose=2)
y_valid_predy_valid_pred는 교차 검증을 통해 구한 모의고사 정답 값
MAE(Mean Absolute Error)
- 모델의 예측값과 실제 값 차이의 절대값 평균
- 절대값을 취하기 때문에 가장 직관적임
# mean_absolute_error
mae = abs(y_train - y_valid_pred).mean()from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_train, y_valid_pred)MSE(Mean Squared Error)
- 모델의 예측값과 실제값 차이의 면적의(제곱)합
- 제곱을 하기 때문에 특이치에 민감하다.
# mean_squared_error
mse = np.square(y_train - y_valid_pred).mean()from sklearn.metrics import mean_squared_error
mean_squared_error(y_train, y_valid_pred)RMSE(Root Mean Squared Error)
- MSE에 루트를 씌운 값
- RMSE를 사용하면 지표를 실제 값과 유사한 단위로 다시 변환하는 것이기 때문에 MSE보다 해석이 더 쉽다.
- MAE보다 특이치에 Robust(강하다 ==덜 민감하다)
RMSE = np.sqrt(mse)mse ** 0.5rmse = np.square(y_train - y_valid_pred).mean() ** 0.5RMSLE(Root Mean Squared Log Error)

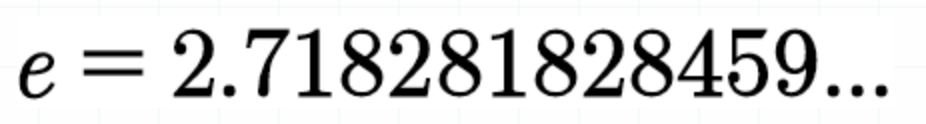
- x 가 1보다 작으면 음수가 나오기 때문에 1을 더해서 1이하의 값이 나오지 않게 하기위해 1을 더한 후에 로그를 취한다.
- log의 밑은 e로 자연상수이다 (더 읽어보기 : https://sseong40.tistory.com/2)
- RMSLE는 예측과 실제값의 "상대적" 에러를 측정해준다.
- RMSLE는 실제값보다 예측값이 클떄보다, 실제값보다 예측값이 더 작을 때 (Under Estimation) 더 큰 패널티를 부여한다.
- RMSE: 오차가 클수록 가중치를 주게 됨(오차 제곱의 효과)
- RMSLE: 오차가 작을수록 가중치를 주게 됨(로그의 효과)
from sklearn.metrics import mean_squared_log_error
mean_squared_log_error(y_train, y_valid_pred) ** 0.5rmsle = np.sqrt(np.square(np.log(y_train+1) - np.log(y_valid_pred +1)).mean())
로그 참고
# np.log(x + 1) == np.log1p(x)