최적화란?
최적화(Optimization)란 손실함수(Loss Function)값을 최소화하는 파라미터를 구하는 과정이다.
이때 손실함수는 예측값과 실제 정답값의 차이를 의미한다.
Gradient Descent(경사하강법)의 정의
gradient는 기울기, 경사를 의미하며 경사하강법의 주된 목적은 함수의 최소값을 찾는 것이다.
이에 따라, 경사하강법은 기울기가 작아지는 방향을 찾고 해당 방향으로 한 걸음 씩 계속 내딛으면서
값이 제일 작은 곳을 찾아 나가는 방법이다.
💡 함수 최소값 탐색에 미분계수가 0이 되는 지점을 찾지 않고 GD 사용하는 이유는?
- 우리가 주로 실제 분석에서 맞닥뜨리게 되는 함수들은 닫힌 형태(closed form)가 아니거나 함수의 형태가 복잡해 (가령, 비선형함수) 미분계수와 그 근을 계산하기 어려운 경우가 많고,
- 실제 미분계수를 계산하는 과정을 컴퓨터로 구현하는 것에 비해 gradient descent는 컴퓨터로 비교적 쉽게 구현할 수 있기 때문이다.
- 데이터 양이 매우 큰 경우 gradient descent와 같은 iterative한 방법을 통해 해를 구하면 계산량 측면에서 더 효율적으로 해를 구할 수 있다.
학습률 (LearningRate)
경사하강법이 기울기가 감소하는 방향으로 한 걸음씩 내딛는 것이라면, 어떤 보폭으로 걸을 것이지도 중요할 것이다. 이때 보폭을 결정하는 것이 바로 학습률(learning rate), 다른 말로 step size라고 한다.
1️⃣ Step size가 큰 경우
한 번 이동하는 거리가 커지므로 빠르게 최소값에 수렴할 수 있다는 장점이 있다.
하지만, 너무 크게 설정해버리면 최소값이 되는 지점을 지나쳐버리고 결국에는 함수 값이 계속 커지는 방향(즉 발산)으로 최적화가 진행될 수 있다.
2️⃣ Step size가 작은 경우
한 번 이동하는 거리가 적기 때문에 꼼꼼하게 최소값을 탐색할 수 있을 것이다.
하지만, 너무 작게 설정해버리면 시간이 매우 오래 걸릴 것이다.
💡 적절한 크기의 step size를 결정하는 것이 매우 중요하다.
Stochastic Gradient Descent (SGD)
데이터가 굉장히 클 경우 모든 데이터에 대한 gradient를 구할 수 없을 것이다.
전체 중 일부만 추출해서 사용하고자 하는 것이 바로 Stochastic Gradient Descent, SGD이다.

Stochastic Gradient Descent 작동 원리
1️⃣ 전체 데이터를 N등분 한다. (등분한 데이터 한 그룹을 batch라고 표현한다.)
2️⃣ 첫 번째 batch에 gradient descent를 적용한 후 update한다.
3️⃣ 업데이트 한 값을 기반으로, 다시 두 번째 batch에 gradient descent를 적용한 후 update한다.
4️⃣ N 번째 batch까지 2️⃣3️⃣ 과정을 반복한다.
Stochastic Gradient Descent 장점
SGD를 사용하면 full gradient가 한 번 업데이트하는 동안에 batch size만큼 업데이트 할 수 있게 되고, 훨씬 빠르게 해를 구할 수 있게 된다. (이런 장점 덕분에 빅데이터에서 SGD를 많이 사용함)
Batch size의 결정
정말 극단적으로 데이터 하나만을 이용해서 Gradient를 구하고 모든 데이터에 대해 한 번씩 업데이트를 해줄 수도 있긴 할 것이다. 그러나, 하나만 가지고 추정하기에는 부정확도가 매우 클 것이다. 따라서 어느 정도로 큰 batch size로 SGD를 진행하는 것이 바람직하다.
SGD 내용 출처_[K-mooc] Model learning with Optimization_데이터공부맛집
경사하강법의 문제점과 Momentum
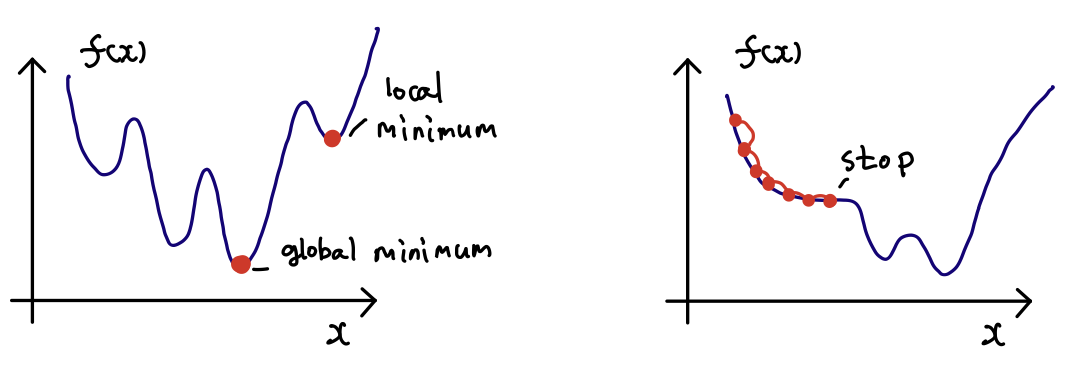
1️⃣ local minimum은 구할 수 있지만 global minimum을 확실하게 찾을 수는 없다.

SGD를 사용하면 꽤 좋은 local minimum을 찾을 수는 있지만, 그 값이 global minimum이라는 것은 보장할 수 없다.
Global Minimum은 목표 함수 그래프 전체를 고려했을 때 최솟값을 의미하고, Local minimum은 그래프 내 일부만 고려했을 때 최솟값을 의미한다.
2️⃣ 수렴속도가 느리다.
학습률이 함수를 넘어 지나치거나 심지어 함수값이 증가하여 수렴하지 않을 수도 있고,
반대로 너무 작으면 수렴하는 속도가 느릴 수 있다.
3️⃣ 안정점(Saddle point)를 벗어나지 못한다.
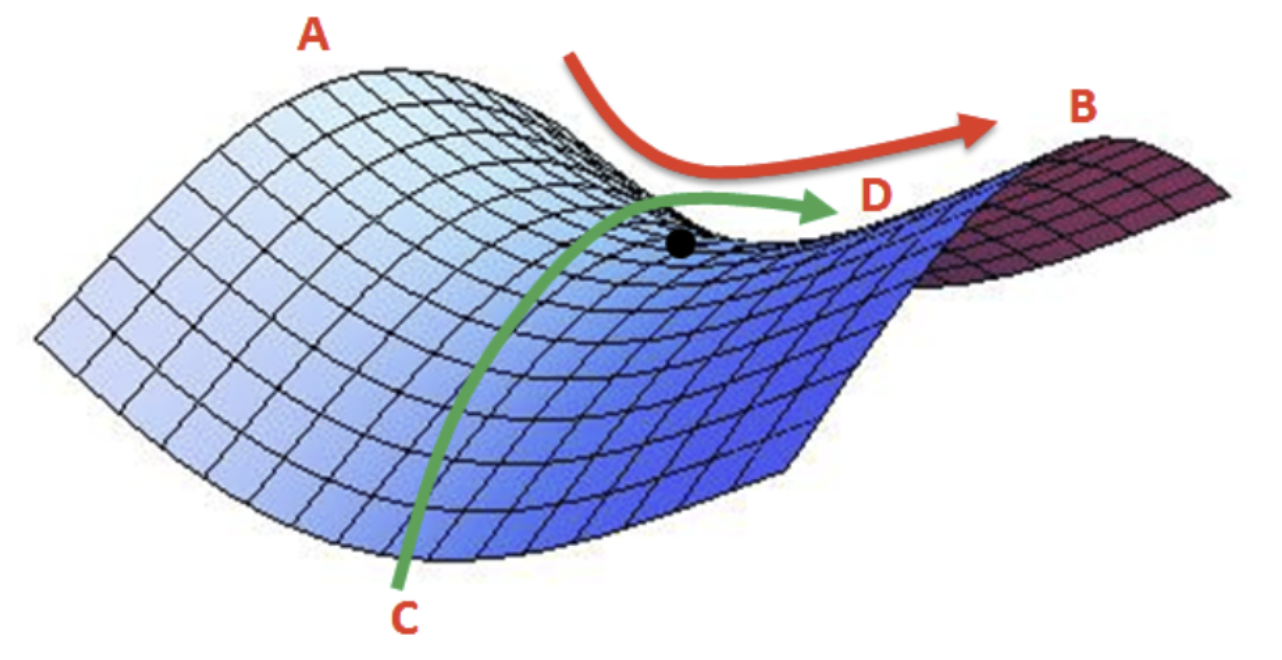
위의 그림에서 검정색 점이 안장점이며 기울기가 0이지만 극값이 아닌 지점을 의미한다.
A-B 사이에서 검은색 점은 최솟값(minima)이지만, C-D 사이에서 검은색 점은 최댓값(maxima)이다. 따라서 해당 지점은 미분이 0이지만 극값을 가질 수 없다. 경사 하강법은 미분이 0일 경우 더이상 파라미터를 업데이트하지 않기 때문에, 이러한 안장점을 벗어나지 못하는 한계가 있다. 출처_[Deep Learning] 최적화(Optimizer): (1) Momentum
💡 이런 단점을 보완하고자 사용하는 것이 바로 'Momentum'이다.
모멘텀 (Momentum)
모멘텀은 경사하강법 (Gradient Descent Method) 통해 W(기울기)가 이동하는 과정에서 일종의 '관성'을 부여하는 것이다. 즉 W를 업데이트 할 때에 이전 단계의 업데이트 방향을 반영하는 것이다. 하지만 Momentum에도 단점이 있는데, W를 업데이트 할 때마다, 과거에 이동했던 양을 변수별로 저장해야하므로 변수에 대한 메모리가 2배로 소모된다는 것이다.
Nesterov 모멘텀 (네스테로프)

모멘텀 방식을 기초로 하지만, 모멘텀을 약간 변형한 것이 Nesterov 모멘텀이다.
Nesterov 모멘텀은 모멘텀에 의해 연두색 화살표의 끝점으로 이동한 후, 그 위치에서 그라디언트를 계산하여 W를 갱신하는 방법이다.
실제로 그냥 모멘텀보다 Nesterov 모멘텀이 더 널리 사용되고 있다고 한다.
출처_[신경망] 4. 경사하강법 (Gradient Descent) (3) Momentum_분석벌레의공부방
